La estadistica es una rama de las matematicas que utiliza grandes conjuntos de datos numericos para obtener conclusiones basadas en distintos calculos.
ESTADISTICA DESCRIPTIVA
Que se ocupa de organizar, resumir y describir las características de conjuntos de datos mediante presentaciones graficas o numericas.
POBLACION
Es la coleccion de objetos acerca de los cuales se desea obtener informacion.
MUESTRA
Es una parte representativa de la poblacion.
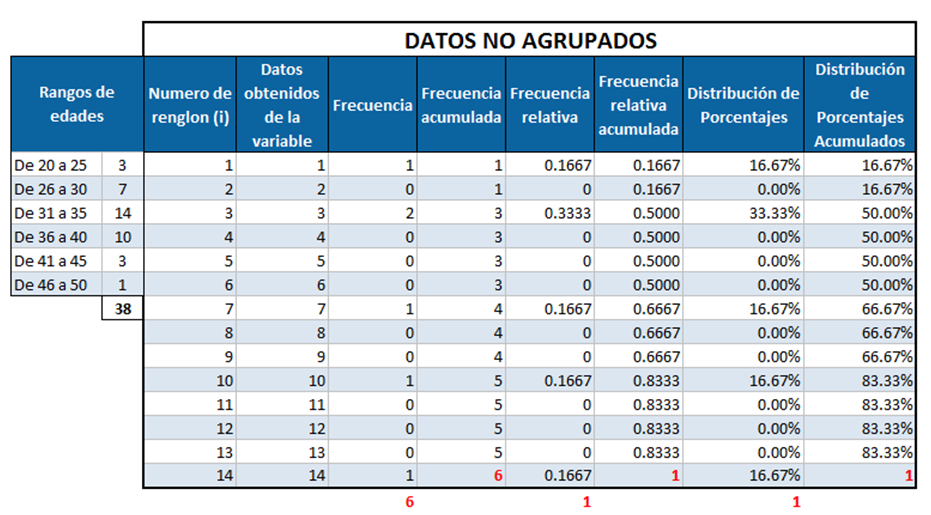
DATOS NO AGRUPADOS
Son los que se dan por medio de una lista completa uno por uno.
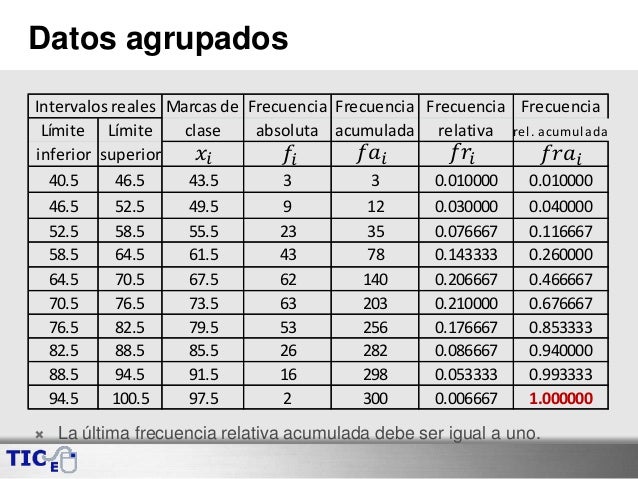
DATOS AGRUPADOS
Se presentan en tablas de frecuencia las cuales solo una representacion conjunta en formato de tabla de datos y su ordenamiento
http://132.248.164.227/publicaciones/docs/apuntes_matematicas/34.%20Estadistica%20Descriptiva.pdf
MEDIDAS DE TENDENCIA CENTRAL MARLEN FRUCTUOSO #13
Las medidas de tendencia central, nos facilitan información de un conjunto o serie de datos que estamos analizando, una vez que estos fueron recopilados u organizados.
MEDIA
Es la suma de los valores de todas las observaciones, dividida entre el número de observaciones realizadas. Se denota generalmente como x.
MEDIANA
Es el valor central que se localiza en una serie ordenada de datos. Se representa con "Md".
Cuando hay un conjunto de datos y se encuentran dos datos en el centro se divide entre 2.
MODA
Es el valor más frecuente en una serie de datos. Se representa con "Mo". Si tienen dos modas se llamará bimodal y si se tiene más de dos se denota multimodal. 
Para más información consultar en: http://asesorias.cuautitlan2.unam.mx
Medidas de dispersión arleth ximena #5
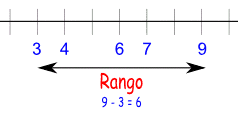
RANGO
Indica la dispersión entre los valores extremos de una variable. se calcula como la diferencia entre el mayor y el menor valor de la variable. Se denota como R.
Para datos ordenados se calcula como:
R = x(n) - x(1)
Donde: x(n): Es el mayor valor de la variable. x(n): Es el menor valor de la variable.
Varianza
La varianza de una variable aleatoria es una medida de dispersión definida como la esperanza del cuadrado de la desviación de dicha variable respecto a su media. O en pocas palabras, es la media de los residuos al cuadrado.
Su unidad de medida corresponde al cuadrado de la unidad de medida de la variable: por ejemplo, si la variable mide una distancia en metros, la varianza se expresa en metros al cuadrado. La varianza tiene como valor mínimo 0. La desviación estándar (raíz cuadrada de la varianza) es una medida de dispersión alternativa, expresada en las mismas unidades que los datos de la variable.
 DESVIACIÓN TÍPICA O ESTÁNDAR HERNÁNDEZ TRUJILLO FRIDA #21
La desviación estándar es la medida de dispersión más común, que indica qué tan dispersos están los datos con respecto a la media. Mientras mayor sea la desviación estándar, mayor será la dispersión de los datos.
La desviación estándar o desviación típica es la raíz cuadrada de la varianza.
Es decir, la raíz cuadrada de la media de los cuadrados de las puntuaciones de desviación.
La raíz cuadrada positiva de la varianza se denomina desviación estándar y se denota con S.
La característica de la desviación estándar de tener la misma unidad que los datos, hace que sea más utilizada como medida de dispersión que la varianza.
EJEMPLO:
1.- En el primer ejemplo del subtema anterior, tenemos que: S = (raíz cuadrada) de: 4.4 = 2.09.https://www.youtube.com/watch?v=YC9158GWkpY  |
A veces se requiere de un minucioso estudio del contenido de las tablas de frecuencia para descubrir la informacion que traen los datos,en tanto que,si seleccionamos apropiadamente una representacion grafica de este contenido,la informacion emerge con mayor claridad.por este motivo vamos a aprender a representar graficamente la tabla de distribuciones.
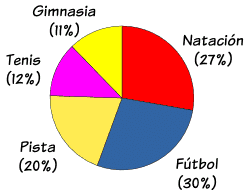
DE PASTEL
Es un circulo que se divide en porciones,se emplean para representar variables cualitativas o categoricas.El area de cada parte o sector del circulo esta directamente relacionado con la frecuencia del dato representado.
para determinar el angulo del sector circular se debe realizar la siguiente formula
grados del sector: (f)(360º)
---------------
la suma de f
Ejemplo
En una clase de 30 alumnos, 12 juegan a baloncesto, 3 practican la natación, 4 juegan al fútbol y el resto no practica ningún deporte.
Para mas informacion consulta la pagina https://www.chartblocks.com/es/charts/chart/type/pie-chart
DE BARRAS:
Se recomienda emplear para datos cualitativos discretos.Se conforma por medio de rectangulos separados de una unidad cuya base es cada uno de los datos y su altura la frecuencia que le corresponda.
|
El diagrama de barras asociado es:
 |
Para mas informacion consulta la pagina https://es.schoolofdata.org/de-los-datos-a-los-graficos/
HISTOGRAMAS
es una grafica conformada por barras que tienen como base un intervalo de clase y como altura la frecuencia del intervalo.
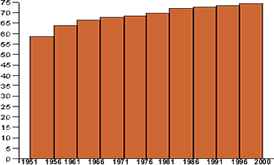
Histograma con intervalos constantes
La esperanza de vida de un hombre al nacer viene dada por la tabla que se adjunta, como se observa los intervalos en que se divide son de amplitud constante, entonces se puede representar el histograma correspondiente tomando
|  |
Para mas informacion consulta http://www.hrc.es/bioest/Ejemplos_histo.html
No hay comentarios.:
Publicar un comentario